Le principe | les calculs | la droite de hauteur
Le principe de la navigation Astronomique:
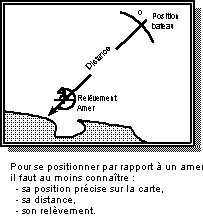
Supposez que vous êtes au large d'une
côte, sur laquelle vous apercevez un seul amer, un phare par exemple. Pouvez-vous
en une seule observation, vous situez par rapport à cet amer ? Oui, à condition
de connaître trois choses :
Si vous pouvez déterminer ces 3 éléments (en reconnaissant le phare, puis en mesurant son relèvement au compas et sa distance... au télémètre, par exemple...), vous pouvez vous situer par rapport à lui : "Je suis à x milles du phare Machin, dans telle direction"....
Si on est sûr ca suffit, sinon on recommencera avec 2 autres phares pour faire un chapeau dont on causera plus tard.
C'est exactement ce principe que nous allons utiliser en navigation astronomique.
 Une fois l'observation faite, nous disposons de deux
données numériques précises :
Une fois l'observation faite, nous disposons de deux
données numériques précises :
1 - L'heure G.M.T. de l'observation va nous servir à calculer un amer virtuel : la position exacte du soleil à l'instant de la mesure.
Vous donnez à votre ordinateur la date et l'heure G.M.T. de l'observation, et il calcule immédiatement la position de l'astre à cet instant.
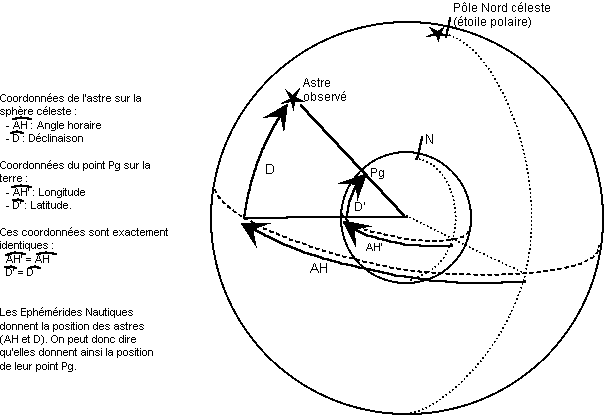
La position de l'astre ainsi calculée est aussi celle de son "pied" à la surface du globe. Cela signifie que, si à l'instant de votre mesure au sextant, un observateur s'était trouvé sur la terre à l'endroit précis dont vous venez de calculer les coordonnées, il aurait vu l'astre que vous avez visé très exactement au-dessus de sa tête, à sa verticale, à son zénith.
Ce point particulier, le "pied" de l'astre à l'instant de la mesure, est appelé point sans ombre ou Position géographique de l'astre. En abrégé : Pg.
Voyez le module position du Soleil pour visualiser le point Pg avec NAVASTRO.
C'est par rapport à ce point de la surface du globe que nous allons nous situer.
Il nous faut maintenant connaître la distance exacte qui sépare notre position (d'où nous avons visé l'astre) de ce point Pg. Cette distance est probablement très grande : quelques milliers de milles nautiques, sûrement.
2 - C'est l'angle mesuré au sextant qui va nous nous permettre de calculer cette distance.
Il faut d'abord corriger la mesure donnée par le sextant (appelée Hauteur instrumentale Hi). En effet cette mesure est entachée de quelques erreurs naturelles inévitables dues à la réfraction de l'atmosphère, à notre position quelques mètres au-dessus de la surface de la mer (pourvu que ça dure)...
La hauteur ainsi corrigée devient alors la Hauteur Vraie Hv
Nota : Dans le schéma qui suit le soleil est considéré à l'infini, ce qui est faux, donc une erreur supplémentaire est automatiquement prise en compte par le logiciel (la parallaxe)
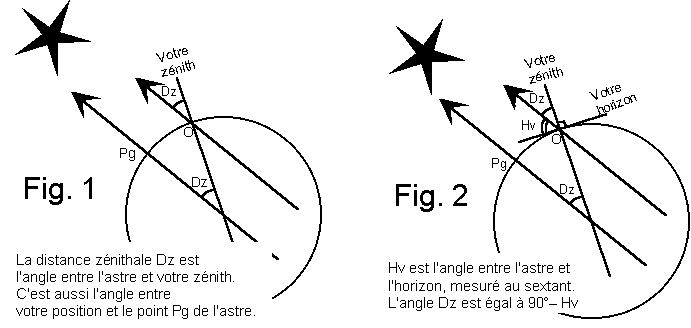
La distance exacte au mille près qui nous sépare de Pg est égale à : 90° – Hv
Exemple : Vous avez mesuré la hauteur du soleil au sextant, et, après correction, vous avez obtenu une hauteur vraie Hv = 37° 28'. La distance zénithale est donc de : 90°-37°28' = 52°32' soit, converti en minutes : (52x60)+32=3152'. Sachant que, par définition, un mille nautique égale une minute d'arc de grand cercle, nous pouvons dire que, à l'instant de la mesure, nous étions exactement à 3152 milles nautiques de Pg.
Nous connaissons donc maintenant 2 éléments précis : les coordonnées du point Pg, et la distance qui nous en sépare. Nous pourrions donc placer sur une planisphère le point Pg, mesurer au compas de relèvement la direction de l'astre observé, tracer cette direction sur notre planisphère en passant par Pg, et enfin porter la distance zénithale le long de cette droite. Le point ainsi obtenu serait notre position.
Malheureusement, cette méthode est inapplicable car beaucoup trop imprécise. Il a donc fallu inventer une méthode qui permette de tracer la position sur la carte de la zone où on navigue et sur laquelle le point Pg ne peut pas apparaître car beaucoup trop éloigné. Cette méthode, c'est la droite de hauteur, mise au point par l'amiral Marc de Saint Hilaire en 1875.
Le point Pg étant inaccessible car beaucoup trop éloigné, l'idée a été de retourner le problème et de partir de la position estimée du bateau. Autrement dit, le raisonnement est le suivant :
Je suppose que je suis à l'endroit O. Si j'étais vraiment à cet endroit, j'aurais dû mesurer l'astre à une hauteur Hc (que je peux calculer grâce à des formules de maths). Or, en réalité, j'ai mesuré l'astre avec mon sextant à la hauteur Hv. Comment utiliser ces deux mesures pour rectifier ma position ?
Pour comprendre cela, il faut bien comprendre la relation étroite entre la hauteur de l'astre et sa distance zénithale. Imaginons que je mesure un astre à une hauteur H. Ma distance zénithale serait alors 90°– H. Mais si je me rapproche de Pg de 1 mille, ma distance zénithale va diminuer de 1 mille. Donc, et puisque la relation Dz = 90° – H reste vraie, c'est que l'astre va m'apparaître plus haut de 1 minute d'arc. H sera alors de H+1'
Inversement, si je m'éloigne de Pg de, disons, 10 milles. Ma distance zénithale va augmenter de 10 milles et donc la hauteur à laquelle l'astre m'apparaîtra diminuera de 10 minutes d'arc. H sera alors de H – 10'
Enfin, si je me déplace sur la droite ou sur la gauche en restant toujours à la même distance de Pg, il est évident que l'astre m'apparaîtra toujours à la même hauteur. Je pourrais ainsi parcourir un immense cercle dont Pg serait le centre et Dz (Distance zénithale) le rayon, et sur lequel l'astre m'apparaîtrait toujours à la même hauteur. C'est le "cercle de hauteur".
Ainsi, la différence entre les deux hauteurs (Hc et Hv) exprimée en minutes d'arc m'indique exactement la distance en milles séparant ma position estimée (où je crois être) de mon cercle de hauteur vraie (où je suis réellement). Cette mesure est l'intercept.
Ces deux mesures ont un point de départ commun : la position Pg de l'astre. Je dois donc maintenant déterminer avec précision dans quelle direction se trouve Pg par rapport à ma position estimée.
Pour cela, il est tout à fait possible de mesurer au compas de relèvement la position de l'astre. Mais outre qu'il est dangereux de regarder le soleil sans protection, cette mesure au compas est trop imprécise. On préfère donc calculer aussi cette valeur. C'est l'azimut.